GLE Example: curvedarrow.gle

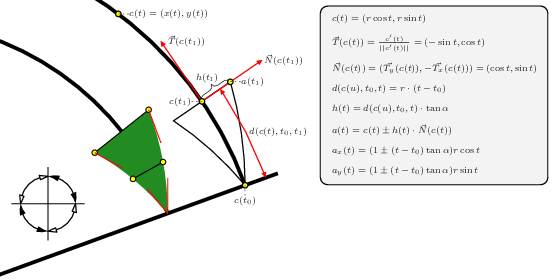
[PDF file]

 

---

size 15 7.5

include "shape.gle"

! extra space between rows in LaTeX table (on the right)
begin texpreamble
   \usepackage{tabls}
   \setlength{\tablinesep}{0.3cm}
end texpreamble

! draw tiny dotted lines between point and corresponding label
sub hair_line dx dy
   gsave
   set lwidth 0.0125 lstyle 2
   rline dx dy
   grestore
   rmove dx dy
end sub

! draw a small circle filled yellow
sub yellow_circle x y
   amove x y
   circle 0.075 fill yellow
end sub

! set the opening angle and size of the arrow
sub set_arr_angle_size ang siz
   tan_alpha = tan(torad(ang))
   arr_angle = ang
   arr_size  = siz
end sub

! get the value of "t1" given the arrow length
sub get_delta_theta arrlen
   side = arrlen * cos(torad(arr_angle))
   return todeg(side/r)
end sub

! evaluate a degree 5 polynomial
sub ev5 a5 a4 a3 a2 a1 a0 x
   return a5*x^5 + a4*x^4 + a3*x^3 + a2*x^2 + a1*x + a0
end sub

! evaluate the first derivative of a degree 5 polynomial
sub ev5p a5 a4 a3 a2 a1 a0 x
   return 5*a5*x^4 + 4*a4*x^3 + 3*a3*x^2 + 2*a2*x + a1
end sub

! compute the norm of a given vector
sub norm x1 y1
   return sqrt(x1^2+y1^2)
end sub

! compute the x-coordinate of a point on the arrow side
sub ax t0 t pm
   return (1+pm*(t-t0)*tan_alpha)*r*cos(t)
end sub

! compute the y-coordinate of a point on the arrow side
sub ay t0 t pm
   return (1+pm*(t-t0)*tan_alpha)*r*sin(t)
end sub

! compute the first derivative of the x-coordinate of the arrow side
sub apx t0 t pm
   return r*(-sin(t)+pm*tan_alpha*(cos(t)-t*sin(t)+t0*sin(t)))
end sub

! compute the first derivative of the y-coordinate of the arrow side
sub apy t0 t pm
   return r*(cos(t)+pm*tan_alpha*(sin(t)+t*cos(t)-t0*cos(t)))
end sub

! normalized first derivative of the x-coord of the arrow side
sub apx_norm t0 t pm pm2
   local tx = apx(t0,t,pm2)
   local ty = apy(t0,t,pm2)
   local d = norm(tx,ty)
   return pm*tx/d
end sub

! normalized first derivative of the y-coord of the arrow side
sub apy_norm t0 t pm pm2
   local tx = apx(t0,t,pm2)
   local ty = apy(t0,t,pm2)
   local d = norm(tx,ty)
   return pm*ty/d
end sub

! compute a bezier curve through a given point
! assume two control points at same distance from the end points
sub bezier_slope_pt x0 y0 dx1 dy1 dx2 dy2 x3 y3 xp yp
   local a = xp - x0
   local b = 3*(x0-x3)
   local c = 2*(x3-x0)
   local d = dx1
   local e = dx2 - 2*dx1
   local f = dx1 - dx2
   local g = yp - y0
   local h = 3*(y0-y3)
   local i = 2*(y3-y0)
   local j = dy1
   local k = dy2 - 2*dy1
   local l = dy1 - dy2
   local a5 = c*l - i*f
   local a4 = c*k + b*l - i*e - h*f
   local a3 = c*j + b*k - i*d - h*e
   local a2 = b*j + a*l - h*d - g*f
   local a1 = a*k - g*e
   local a0 = a*j - g*d
   local t  = 0.5
   local tp = 0
   while abs(t-tp) > 1e-6
      tp = t
      t = t - ev5(a5,a4,a3,a2,a1,a0,t)/ev5p(a5,a4,a3,a2,a1,a0,t)
   next
   local aa = (a + b*t^2 + c*t^3)/(d + e*t + f*t^2)/(3*t)
   asetpos x0 y0
   bezier x0+aa*dx1 y0+aa*dy1 x3+aa*dx2 y3+aa*dy2 x3 y3
   return aa
end sub

! draw the curved arrow head
sub curved_arrow_head x0 y0 a1 a2 deco outline
   t0 = torad(a1)
   tm = torad((a1 + a2)/2)
   t1 = torad(a2)
   ! top side (pm = +1)
   local dx11  = apx_norm(t0,t1,-1,+1)
   local dy11  = apy_norm(t0,t1,-1,+1)
   local dx21  = apx_norm(t0,t0,+1,+1)
   local dy21  = apy_norm(t0,t0,+1,+1)
   local x01   = ax(t0,t1,+1) + x0
   local y01   = ay(t0,t1,+1) + y0
   local x31   = ax(t0,t0,+1) + x0
   local y31   = ay(t0,t0,+1) + y0
   local xp1   = ax(t0,tm,+1) + x0
   local yp1   = ay(t0,tm,+1) + y0
   ! bottom side (pm = -1)
   local dx12  = apx_norm(t0,t0,+1,-1)
   local dy12  = apy_norm(t0,t0,+1,-1)
   local dx22  = apx_norm(t0,t1,-1,-1)
   local dy22  = apy_norm(t0,t1,-1,-1)
   local x02   = ax(t0,t0,-1) + x0
   local y02   = ay(t0,t0,-1) + y0
   local x32   = ax(t0,t1,-1) + x0
   local y32   = ay(t0,t1,-1) + y0
   local xp2   = ax(t0,tm,-1) + x0
   local yp2   = ay(t0,tm,-1) + y0
   ! only draw the outline or fill it in green?
   if outline = 1 then
      begin path stroke
         local aa1 = bezier_slope_pt(x01,y01,dx11,dy11,dx21,dy21,x31,y31,xp1,yp1)
         local aa2 = bezier_slope_pt(x02,y02,dx12,dy12,dx22,dy22,x32,y32,xp2,yp2)
         closepath
      end path
   else
      print "dx1 " dx11 " dy1 " dy11 " dx2 " dx21 " dy2 " dy21
      begin path fill forestgreen
         local aa1 = bezier_slope_pt(x01,y01,dx11,dy11,dx21,dy21,x31,y31,xp1,yp1)
         local aa2 = bezier_slope_pt(x02,y02,dx12,dy12,dx22,dy22,x32,y32,xp2,yp2)
         closepath
      end path
   end if
   ! draw decorations?
   if deco = 1 then
      gsave
      set color black lwidth 0.025
      amove x01 y01
      aline x32 y32
      amove xp1 yp1
      aline xp2 yp2
      yellow_circle x01 y01
      yellow_circle xp1 yp1
      yellow_circle x32 y32
      yellow_circle xp2 yp2
      set color red
      amove x01 y01
      aline x01+dx11*aa1 y01+dy11*aa1
      amove x31 y31
      aline x31+dx21*aa1 y31+dy21*aa1
      amove x02 y02
      aline x02+dx12*aa2 y02+dy12*aa2
      amove x32 y32
      aline x32+dx22*aa2 y32+dy22*aa2
      grestore
   end if
   ! name some crucial points on the arrow head
   amove x0+r*cos(torad(a2)) y0+r*sin(torad(a2))
   save tcenter
   rmove -2*sin(torad(a2)) 2*cos(torad(a2))
   save ttangent
   amove x01 y01
   save tnormal
   amove x31 y31
   save btip
end sub

! some general settings
set lwidth 0.1 join mitre
set_arr_angle_size 20 2.75

a1 = 20
r  = +8
x0 = -3
y0 = -1

! draw a line at angle 20 degrees
amove x0 y0
aline x0+(r+3.2)*cos(torad(a1)) y0+(r+3.2)*sin(torad(a1))

! draw the first arc
amove x0 y0
arc r a1 90

! draw the arc's arrow head
a2 = a1+get_delta_theta(2.75)
curved_arrow_head x0 y0 a1 a2 1 0

! draw another arc and arrow head
r = +10.25
set color black
amove x0 y0
arc r a1 90
set lwidth 0.03
a2 = a1+get_delta_theta(2.75)
curved_arrow_head x0 y0 a1 a2 0 1

! draw the math equation of the curve
yellow_circle x0+r*cos(torad(53)) y0+r*sin(torad(53))
hair_line 0.3 0
set just lc arrowsize 0.15 arrowangle 25 hei 0.25
tex "$c(t) = (x(t),y(t))$"

! annotate with the "tangent"
set color red
amove ptx(tcenter)  pty(tcenter)
aline ptx(ttangent) pty(ttangent) arrow end
rmove 0.2 0
set color black
tex "$\vec{T}(c(t_1))$"

nx = ptx(tnormal)-ptx(tcenter)
ny = pty(tnormal)-pty(tcenter)
d  = norm(nx,ny)
nx = nx/d; ny = ny/d

! annotate with the "normal"
set color red
amove ptx(tcenter)  pty(tcenter)
aline ptx(tcenter)+nx*2 pty(tcenter)+ny*2 arrow end
rmove 0.05 0
set color black
tex "$\vec{N}(c(t_1))$"

! annotate with the distance along the arc
set color red
amove x0 y0
d = 0.6
arc r+d a1 a2 arrow both
set color black
amove x0+(r+d)*cos(torad((a1+a2)/2))+0.1 y0+(r+d)*sin(torad((a1+a2)/2))
tex "$d(c(t),t_0,t_1)$"

! annotate with the height
gsave
set lwidth 0.0125 just bc
curly_bracket ptx(tcenter) pty(tcenter) ptx(tnormal) pty(tnormal) 0.12
amove (ptx(tcenter)+ptx(tnormal))/2-0.25 (pty(tcenter)+pty(tnormal))/2+0.25
tex "$h(t_1)$"
grestore

! indicate points t0 and t1 on the arrow head
yellow_circle ptx(btip) pty(btip)
hair_line 0 -0.3
set just tc
tex "$c(t_0)$"
yellow_circle ptx(tcenter) pty(tcenter)
hair_line -0.3 0
set just rc
tex "$c(t_1)$"
yellow_circle ptx(tnormal) pty(tnormal)
hair_line 0.3 0
set just lc
tex "$a(t_1)$"

! add all mathematical equations
set just tr
amove pagewidth()-0.2 pageheight()-0.2
begin box add 0.1 fill rgb255(240,240,240) round 0.2
   begin tex
      \begin{tabular}{l}
      $c(t) = (r\cos{t},r\sin{t})$\\
      $\vec{T}(c(t)) = \frac{c'(t)}{||c'(t)||} = (-\sin{t},\cos{t})$  \\
      $\vec{N}(c(t)) = (\vec{T_y}(c(t)), -\vec{T_x}(c(t))) = (\cos{t},\sin{t})$\\
      $d(c(u),t_0,t) = r\cdot(t-t_0)$\\
      $h(t) = d(c(u),t_0,t)\cdot\tan{\alpha}$\\
      $a(t) = c(t) \pm h(t) \cdot \vec{N}(c(t))$\\
      $a_x(t) = (1 \pm (t-t_0)\tan{\alpha}) r \cos{t}$\\
      $a_y(t) = (1 \pm (t-t_0)\tan{\alpha}) r \sin{t}$\\
      \end{tabular}
   end tex
end box

! test the arrow functions from GLE
set arrowsize 0.3 arrowangle 15
amove 0.25 2
aline 2.25 2
amove 1.25 3
aline 1.25 1
amove 1.25 2
set arrowstyle filled
arc 0.75 0   90  arrow both
arc 0.75 180 270 arrow both
set arrowstyle empty
arc 0.75 90  180 arrow both
arc 0.75 270 0   arrow both

---

 

[Return to examples page]